Yıllar, yıllar önce bizi Google ile tanıştıran bu algoritma basitliği sayesinde bir çok probleme deva olmaya devam etmektedir. İşin özüne bakacak olursak, bu algoritmanın yapmaya çalıştığı bir ağ içerisindeki önemli düğümleri bulmaya çalışmaktır.
Tamam da, "önemli" derken neden bahsediyoruz? Kime göre, neye göre önemli? Öncelikle bir düğümü diğerinden daha önemli yapan kriteri belirlememiz gerekir. Şayet boy, pos, para gibi özel niteliklere bakıyor olsaydık basit bir sıralama yapmamız yeterli olacaktı. Ancak, eğer dikkate aldığımız özellikler etkileşimli ise, yani herkesin birbirini etkilediği bir durum söz konusuysa, işler biraz daha karmaşık hale gelecektir.
Eskiden, çok eskiden "web sörfü" diye bir kavram vardı. Hemen her yerde gördüğümüz bu laf bir şekilde kaybolup gitti. Arama motorlarının pek gelişmediği, bir arama motorunda yer almak için kırk takla attığımız günlerde yapabileceğimiz en iyi şey web sayfamıza giden kısayolun mümkün olduğunca başka web sayfalarında yer almasını sağlamak idi. Bunun için çeşitli takibe takip mantığında oluşumlar ile sayfalar bir birilerine ziyaretçi gönderirdi. Bir sörfçü bir sayfadan başlayıp, bu kısayollar ile bir çok siteyi tanırdı.
Böyle bir dünyada önemli web sayfası bariz şekilde kendisine en çok kısayol verilen sayfa olacaktır. Ama dikkat edin, bu link verenlerin de önemli olması gerekir. Onların önemli olması da aynı şekilde çok bağlantı almalarından geçer. Sonuçta zayıf bir çok yerden bağlantı almak yerine güçlü bir kaç yerden bağlantı almak sizi daha güçlü kılacaktır. Bu durum aynı zamanda bir olasılık problemidir zira PageRank herhangi bir sayfadan başlayan yolculuğunuzun ne kadar olasılıkla hedef sayfaya ulaşacağını bulmaya çalışır (Markov Zinciri).
Algoritmanın temel iki versiyonu bulunuyor:
\operatorname{PageRank}(A)=1-d+d \times \sum_{i=1}^{n} \frac{\operatorname{PageRank}\left(P_{i}\right)}{O\left(P_{i}\right)},
\operatorname{PageRank}(A)=\frac{(1-d)}{N}+d \times \sum_{i=1}^{n} \frac{\operatorname{PageRank}\left(P_{i}\right)}{O\left(P_{i}\right)}Eşitliklere göre,
• A : PageRank değeri bulunacak düğüm,
• Pi : diğer düğümler,
• O(Pi) : düğüm Pi’den dışarıya giden hat sayısı,
• d : sönümleme faktörü (genellikle 0.85 alınır),
• N : düğüm sayısı.
İlk yöntemde ortalama PR değeri 1'e yakınsıyorken,ikincide toplam değer 1'e yakınsar. Ben yazının devamında 2. değeri kullanacağım. Sonuçlarını anlamak bana daha kolay geldiği için onu tercih edeceğim. Formüle bakınca öz yinelemeyi görmüşsünüzdür. Bunu ya sonuç 1'e yeterince yakınsayınca ya da yeterince fazla deneme yapınca kıracağız. Öz yineleme esnasında mevcut iterasyon içinde değişen PR değerlerini kullanacağız. Fakat, elaman sayısı çoğaldığında paralel çalışabilmesi için bir önceki iterasyonun sonucunu kullanacak şekilde de geliştirme yapabilirsiniz. Zira algoritmanın ürettiği sonuç bir yerden sonra anlamlı şekilde değişmeyecektir.
Kodlamaya geçmeden önce bir veri uydurup kalem kağıt usulü çözelim.
5 düğümden oluşan bir ağımız olsun, bunları web siteleri, arkadaşlar ya da aklına ne geliyorsa gibi düşünebilirsiniz. Sırasıyla A,B,C,D,E isimlerini verelim. Bunların bir birilerine verdikleri bağlantılar şöyle olsun (bağlantıların yönü önemli):
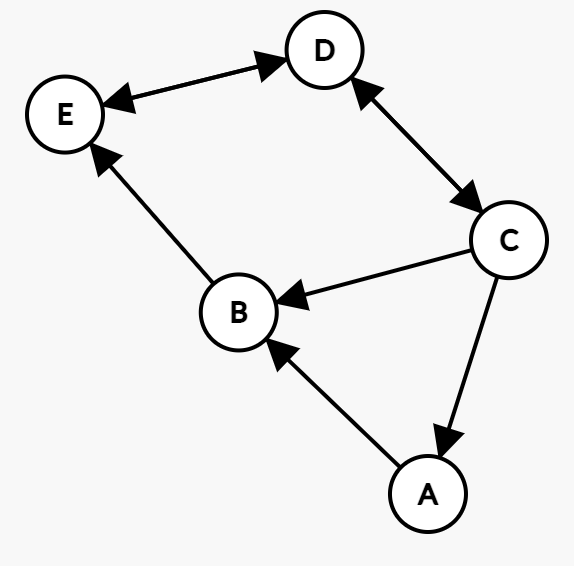
Bu arada bu diyagramı https://csacademy.com/app/graph_editor/ kullanarak çizdim.
Başlangıç değeri herhangi bir sayı olabilir. Her iterasyonda sonuç giderek sabit bir yere varacaktır. Artık ilerleme olmadığını anlamak için bir önceki sonuç ile mevcutu karşılaştırabiliriz veya mevcut sonuçların toplamının 1'e yeterince yakın olup olmadığına bakabiliriz. İlk yöntem daha tutarlı olsa da ikincisi bize performans olarak geri dönecektir.
İlk iterasyonda herkes için page rank değeri 1 olduğu durum ile başlayalım.
A nın değeri için, değişkenleri yerine koyduğumuzda eşitliğimiz şu hale gelecektir (sadece C den 1 lik bağlantı geliyor ve C de 3 farklı yere bağlantı gönderiyor):
\frac{1-0.85}{5}+ 0.85 * \frac{1}{3} = 0.31Aynısını B için yaparsak, A nın değeri artık (0.31) olduğu bilindiği için A'dan gelen kısımda bu değeri kullanacağız ve hesap şu şekilde olacak :
\frac{1-0.85}{5}+ 0.85 * ( \frac{0.31}{1} + \frac{1}{3}) = 0.5796İşlemi tüm düğümler için yaptıktan sonra, Belirleyeceğimiz bir seviyeye kadar tekrar-tekrar değerleri güncelleyeceğiz.
Bunu C# ile koda dökelim.
Öncelikle kişileri tutacak basit bir record hazırlıyoruz.
public record Person(int Id, string Name, HashSet<int> Followers, HashSet<int> Following);Kişinin Id bilgisi kişiler arasında referans olması için kullanılacak. Yukarıdaki şemaya benzer şekilde bir kişi oluşturalım:
Person[] people =
{
new(0, "Ali", new() { 2 }, new() { 1 }),
new(1, "Berk", new() { 0, 2 }, new() { 4 }),
new(2, "Cem", new() { 3 }, new() { 0, 1, 3 }),
new(3, "Doruk", new() { 2, 4 }, new() { 2, 4 }),
new(4, "Erkan", new() { 1, 3 }, new() { 3 })
};Sıra geldi asıl işi yapan koda.
public static Dictionary<Person, double> PageRank(Person[] people, double dampingFactor = 0.85, int maxIterations = 1)
{
const double exitThreshold = 0.001;
var result = people.ToDictionary(x => x, _ => 1.0);
var damping = (1 - dampingFactor) / people.Length;
var peopleDictionary = people.ToDictionary(x => x.Id, x => x);
for (var iteration = 0; iteration < maxIterations; iteration++){
double currentSum = 0;
foreach (var person in people){
var sum = person
.Followers
.Select(x => peopleDictionary[x])
.Sum(x => result[x] / x.Following.Count);
result[person] = damping + dampingFactor * sum;
currentSum += result[person];
}
if (Math.Abs(currentSum - 1) < exitThreshold){
break;
}
}
return result;
}Kod yukarıdan aşağı şöyle akıyor.
- Bir yaklaşma eşiği berlirtiyorum. Şayet sonuç kümesinin toplamı 1'den 0.001 uzaklıktan daha yakın olursa benim için yeterlidir.
- Sonuç sözlüğünü (kümesini) hazırlıyorum. Her kişi için başlangıç PageRank değerini 1 veriyorum.
- Tekrar tekrar yapılacak sönümle işleminin bir parçasını önceden hesaplayıp bir kenara koyuyorum.
- Takip edilen ve takipçi bilgilerini Id üzerinden referanslamıştım, her iterasyonda tekrar tekrar kişileri bulmamak adına Id->Person şeklinde bir index oluşturuyorum.
- Sonuca yaklaşmasa bile belirli bir maksimum deneme sayına kadar deneme yapılması için basit bir for döngüsü kuruyorum
- Mevcut iterasyonun toplam değeri
- Herkesi sırayla dön
- Takip edenler için PR değerini hesapla ve bunu takip edenin takip ettiği kişi sayısına böl
- Sönümleme ve normalizasyon işlemleri
- Toplamı güncelle
- Toplamın 1 e ne kadar uzak olduğına bak, yeterince yakınsa yeni bir iterasyonu gerek yok.
- Sonucu dön
Çıktısı ise şu şekilde olmalı.
Ali : 0,31333333333333335
Berk : 0,5796666666666668
Cem : 0,455
Doruk : 1,0089166666666665
Erkan : 0,95150625Bu kod örneği, küçük boyutlarda oldukça iş görecektir. Fakat, büyük yapılarla çalıştığımız zaman, işleri hızlandırmak için donanımsal hızlandırıcılar kullanmak gerekiyor. C# tarafında bunun için Vector/Matrix tipleri kullanılabilir. Şu örnekte güzel bir çalışma yapılmış:
https://raw.githubusercontent.com/jeffersonhwang/pagerank/master/PageRank.cs
Yine konunun detayları için https://www2.math.upenn.edu/~kazdan/312F12/JJ/MarkovChains/markov_google.pdf ders notlarına bakılabilir.Küçük bir not Markov zincirleri hakkında bir yazı da gelecek.
Kaynaklar ve faydalı içerikler:
http://infolab.stanford.edu/~backrub/google.html
http://delab.csd.auth.gr/~dimitris/courses/ir_spring06/page_rank_computing/01531136.pdf
https://arxiv.org/pdf/1407.5107.pdf



teşekkür ederiz eline emeğine sağlık