Ağları incelemeye devam ediyoruz. PageRank ve ArticleRank'ten sonraki algoritmamız Eigenvector Centrality ya da Özvektör Merkeziliği olacak. Tıpkı ArticleRank'te olduğu gibi temel mantık PageRank ile oldukça benzer olacak. Tabii öncesinde kısaca özvektörleri ve özdeğerleri hatırlamak gerekebilir. Doğrusal cebir'in bu eğlenceli konusu bir çok problemin çözümünde de anahtar rol oynamaktadır. Ana konudan çıkmamak adına özvektör ve değerleri detaya inmeden hızlıca hatırlatacağım.
A * v = \lambda * vBurada A herhangi bir kare matris, v özvektörlerimizden birisi, lambda ise özdeğerlerimizden birisini oluşturuyor. Dikkat ederseniz her ikisi için de çoğul bir ifade kullandım zira A yerine koyacağımız bir kare matris için birden fazla değer/vektör elde edebiliriz. Böyle bir problemi çözmek için denklemi 0'a eşitleyerek başlayabiliriz.
A*v - \lambda * v = 0 \\
(A-\lambda) * v = 0Bir matristen sabit bir sayı çıkmayacağı için lambda değerini A ile aynı boyuttaki birim matris ile çarpıyoruz.
(A - \lambda I) * v = 0Lambda değerini bulmak için de v'yi kaldırıp sol tarafın determinantını almak yetiyor.
|A - \lambda I|= 0Her şeyi yerine koyduğumuzda bir çok değer ve vektör bulacağız ama bizi ilgilendiren bunların en büyüğü (özdeğer) olacak.
Bu vektörü MathNet kütüphanesi kullanarak hızlı bir şekilde bulabilirsiniz. Fakat, ben hazırını göstermeyi sevmediğim için bu değerleri kod yardımıyla bulacağım. Kod yardımıyla en büyük özdeğere karşılık gelen özvektörü bulmak için Power Iteration algoritmasını kullanacağız. Bu algoritmanın özelliği en büyük özdeğer için geçerli olan özvektörlerden birisine doğru giderek yaklaşmasıdır. Aşağıdaki versiyonunda çıkan sonuç en büyük özdeğere karşılık oluşan özvektörün normalize edilmiş halini bulmak için yeterlidir.
private static double[] PowerIteration(double[,] matrix, int maxIterations = 33)
{
var n = matrix.GetLength(0);
var vector = Enumerable.Range(0, n).Select(static _ => Random.Shared.NextDouble()).ToArray();
for (var iteration = 0; iteration < maxIterations; iteration++){
var newVector = MultiplyMatrixByVector(matrix, vector);
newVector = NormalizeVector(newVector);
vector = newVector;
}
return vector;
}Bu kodu açıklayalım:
- Rastgele bir vektör oluşturarak başlıyoruz. İsterseniz tümü 1 olan veya istediğiniz bir vektör ile başlayabilirsiniz.
- Belirlediğimiz iterasyon sayısı kadar ilerliyoruz. Arttırdıkça gerçek değere daha fazla yaklaşırken bir o kadar yavaşlayacağından ihtiyaca yönelik tatlı bir nokta seçebilirsiniz.
- Vektörümüzü matrisimiz ile çarpıyoruz
- Çarpma işleminden sonra çıkan vektör iterasyonlar boyunca büyüyebileceğinden vektörü normalize ediyoruz (uzunluğunu 1'e getiriyoruz)
Tüm işlem bu kadar, fakat performans için bir kaç oyun yapabiliriz. Yapacağımız cinlik, şayet yaklaşma miktarı çok ama çok küçükse boşu boşuna deneme yapmasını engellemek olacak.
Bunu uygularsak döngü kısmımız şu hale gelecektir:
for (var iteration = 0; iteration < maxIterations; iteration++){
var newVector = MultiplyMatrixByVector(matrix, vector);
newVector = NormalizeVector(newVector);
if (newVector.Zip(vector).Sum(v => Math.Abs(v.First - v.Second)) < 0.0000001){
vector = newVector;
break;
}
vector = newVector;
}Sonuca ulaşmanın Inverse Vector Iteration (Gauss Eliminasyonu) gibi yöntemleri de bulunuyor, bunlar donanımsal hızlandırmalar ile daha iyi hale de getirilebilir. Fakat bizim tüm amacımız merkezi bulmak. Yukarıdaki fonksiyonun kullandığı diğer fonksiyonları da şuraya ekleyeyim:
private static double[] MultiplyMatrixByVector(double[,] matrix, double[] vector)
{
var rows = matrix.GetLength(0);
var cols = matrix.GetLength(1);
var result = new double[rows];
for (var i = 0; i < rows; i++){
for (var j = 0; j < cols; j++){
result[i] += matrix[i, j] * vector[j];
}
}
return result;
}
private static double VectorNorm(double[] vector)
{
return Math.Sqrt(vector.Sum(static t => t * t));
}
private static double[] NormalizeVector(double[] vector)
{
var norm = VectorNorm(vector);
return vector.Select(c => c / norm).ToArray();
}Buradan sonra yapacaklarımız için önce örnek teşkil etmesi açısından PageRank'ta kullandığımız değerleri alalım.
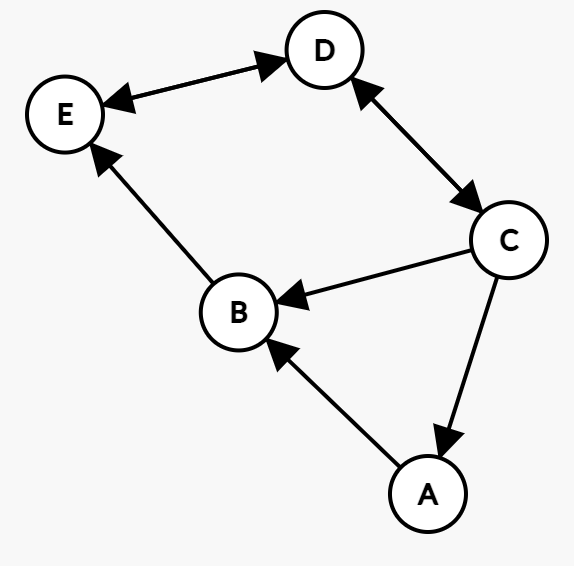
public record Person(int Id, string Name, HashSet<int> Followers, HashSet<int> Following);
Person[] people =
{
new(0, "Ali", new() { 2 }, new() { 1 }),
new(1, "Berk", new() { 0, 2 }, new() { 4 }),
new(2, "Cem", new() { 3 }, new() { 0, 1, 3 }),
new(3, "Doruk", new() { 2, 4 }, new() { 2, 4 }),
new(4, "Erkan", new() { 1, 3 }, new() { 3 })
};Şimdi bu veriyi bir kare matris haline çevirecek bir fonksiyon yazalım.
private static double[,] GetAdjacencyMatrix(Person[] people)
{
var n = people.Length;
var matrix = new double[n, n];
for (var i = 0; i < n; i++){
for (var j = 0; j < n; j++){
matrix[i, j] = people[i].Following.Contains(people[j].Id) ? 1 : 0;
}
}
return matrix;
}Matrisimiz şöyle görünecek:
\begin{matrix}
- & A & B & C& D& E \\
A & 0 & 1 & 0 & 0 & 0 \\
B & 0 & 0 & 0 & 0 & 1 \\
C & 1 & 1 & 0 & 1 & 0 \\
D & 0 & 0 & 1 & 0 & 1 \\
E & 0 & 0 & 0 & 1 & 0
\end{matrix}Daha sonra tek yapmamız gereken bu matrisin özvektörünü bulmak olacak.
var matrix = GetAdjacencyMatrix(people);
var eigenVector = PowerIteration(matrix);
for (var index = 0; index < eigenVector.Length; index++){
var person = people[index];
var t = eigenVector[index];
Console.WriteLine($"{person.Name} : {t}");
}Bunu ekrana bastığımızdaki sonuç ise:
Ali : 0,14686729300051407
Berk : 0,23763628496766961
Cem : 0,6221398443185082
Doruk : 0,6221398680880599
Erkan : 0,3845035669017643Sıralama olarak PageRank ve ArticleRank'e benzer sonuçlar elde ettiğimizi göreceksiniz. PageRank de benzer şekilde matrisler ve özvektörler ile hesaplanabilmektedir.
Bir iki okumalık bırakıyorum:
https://www.ahmeddemir.net/wp-content/uploads/2016/02/Gaussian.pdf
https://people.inf.ethz.ch/arbenz/ewp/Lnotes/chapter7.pdf


